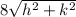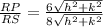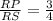Answer:
A.
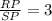
B.
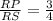
Explanation:
We are given that three collinear points on the coordinate plane are
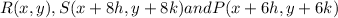
A.We have to find the value of
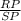
Distance formula :
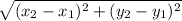
Using this formula and substitute the values then we get
RP=
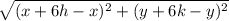
RP=
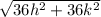
RP=
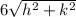
SP=
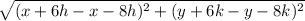
SP=
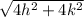
SP=
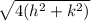
SP=
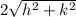
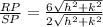
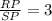
B.We have to determine the value of
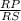
RS=
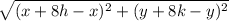
RS=
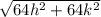
RS=
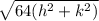
RS=