Question

Part A: Explain why the x-coordinates of the points where the graphs of the equations y= 2-x and y = 8x+4 intersect are the solutions of the equation 2-x=8x+4. (4 points) Part B: Make tables to find the solution to 2-x=8x+4 . Take the integer values of x between −3 and 3. (4 points) Part C: How can you solve the equation 2-x=8x+4 graphically? (2 points)

Answer 1

To find the points where two graphs intersect, we have to equate both expressions together.

To find where y₁ = 2 - x and y₂ = 8x + 4 intersect,

y₁ = y₂

2 - x = 8x + 4

9x = -2

x =
`(9)/(-2) = - (9)/(2) = -4.5`

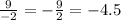
At x = -4.5, both the expressions intersect, that is, have the same y value.

Answer 2

A= Need to find where y^1=2 - x and y^2= 8x + 4 when they intersecect

B= y₁ = y₂

2 - x = 8x + 4

9x = -2
Then,

x= 9/-2 = -9/2= -4.5

C= x= 4.5
So now we know:
Both expressions intersect
Both have the same y value
y=f(x)⟹f(x)=y


Hope this helps you!!!!!!