Question

A highway curve forms a section of a circle. a car goes around the curve. its dashboard compass shows that the car is initially heading due east. after it travels 700. m, it is heading 35.0° south of east. find the radius of curvature of its path. (use the correct number of significant figures.)

Answer 1

The car had traveled 90 - 35 = 55°

Converting to rad:

55° * (2π rad / 360°) = 0.96 rad

length of arc = radius * rad of angle
700 m = R * 0.96
R = 729.17 m

Answer 2

The radius of the curvature is 1145.7 meters.

Explanation:

We are given that,

Distance measured around the curvature, s = 700 meters

Angle measured, θ = 35° = 0.611 radians

Using
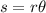`s=r\theta`, we will find the radius of the circle traced by the car.

So, on substituting the values, we get,

`s=r\theta`

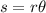
implies
`700=r* 0.611`

i.e.
`r=(700)/(0.611)`

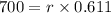
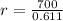
i.e. r = 1145.7 meters.

Hence, the radius of the curvature is 1145.7 meters.