Question

At what points will the line y = x intersect the unit circle x2 + y2 = 1?

Answer 1

We are given the equations:

y = x

x^2 + y^2 = 1

Now to find the points where they will intersect, combine the two equations:

y^2 + y^2 = 1

2 y^2 = 1

y^2 = 0.5

y = 0.707

From equation 1:

x = y = 0.707

Hence the two functions will intersect at:

(0.707, 0.707)

or

(0.7, 0.7)

Answer 2

the line y = x intercept the unit circle x^2+y^2=1 at points:

(0.707, 0.707) and (-0.707, -0.707)

Explanation:

The points of intersection are the points that satisfy the both following equations:

equation 1: y = x

equation 2: x^2 + y^2 = 1

So, we can replace equation 1 on equation 2 as following:

x^2 + y^2 = 1

As well y = x then:

x^2 + x^2 = 1

Isolating x we obtain:

2x^2=1

x^2 = 1/2

`x=\sqrt{(1)/(2) }`

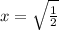
x=±0.707

Taking into account that the squared can be positive or negative, we have two solutions for x: x1=0.707 and x2=-0.707

Finally for find the value of y1 and y2, we replace the value of x1 and x2 on any of the principal equations (equation 1 or 2).

For simplicity we replace on Equation 1 (y = x), so:

y1=x1=0.707 and y2=x2=-0.707

Concluding that the line y = x intercept the unit circle x^2+y^2=1 at points:

(0.707, 0.707) and (-0.707, -0.707)