Question

Can someone please help me with this!!!!

Answer 1

In a triangle the midline joining the midpoints of two sides is parallel to the third side and half as long ⇒

AE = BD*2 = 10*2 = 20
also AE = 2x (given) ⇒
2x = 20
x = 20/2
x = 10

CD = 3x = 3*10 = 30

BD is the midsegment of ΔACE ⇒ ΔBCD ∼ ΔACE therefore:


`(BD)/(CD)= (AE)/(CE) \ \ \ \to \ \ \ CE= (CD*AE)/(BD)= (30*20)/(10)=60`

Answer: 60

Answer 2

You can use the similarity approach of these two triangles CBD and CAE

as a result:

`(BD)/(AE) = (10)/(2x) = (CD)/(CE) = (3x)/(?)`

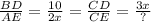
so:
? = 6x^2 / 10 = 0.6 x^2

and the fact of:

"The segment connecting the midpoints of two sides of a triangle is parallel to the third side and equals its half length"

so:BD = 0.5 AE 10 = 0.5 * 2x >>> x= 10


Back to:
? =0.6 x^2 = 0.6 * 10^2 = 0.6 * 100 = 60



A

Hope that helps