Question

The position equation for a particle is s of t equals the square root of the quantity t cubed plus 1 where s is measured in feet and t is measured in seconds. Find the acceleration of the particle at 2 seconds.

1 ft/sec2
two thirds ft/sec2
negative 1 over 108 ft/sec2
None of these

Answer 1

`\bf s(t)=√(t^3+1) \\\\\\ \cfrac{ds}{dt}=\cfrac{1}{2}(t^3+1)^{-(1)/(2)}\cdot 3t^2\implies \boxed{\cfrac{ds}{dt}=\cfrac{3t^2}{2√(t^3+1)}}\leftarrow v(t) \\\\\\ \cfrac{d^2s}{dt^2}=\cfrac{6t(2√(t^3+1))-3t^2\left( (3t^2)/(√(t^3+1)) \right)}{(2√(t^3+1))^2}\implies \cfrac{d^2s}{dt^2}=\cfrac{ (6t(2√(t^3+1))-1)/(√(t^3+1)) }{4(t^3+1)}`


`\bf \cfrac{d^2s}{dt^2}=\cfrac{6t[2(t^3+1)]-1}{4(t^3+1)√(t^3+1)}\implies \boxed{\cfrac{d^2s}{dt^2}=\cfrac{12t^4+12t-1}{4t^3+4√(t^3+1)}}\leftarrow a(t)\\\\ -------------------------------\\\\a(2)=\cfrac{215~ft^2}{44~sec}`

Answer 2

Acceleration of the particle is two thirds ft/s².

Explanation:

It is given that, the position of the particle at time t is given by :

`s(t)=√(t^3+1)`

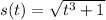
Where

s is in feet

t is in seconds

We need to find the acceleration of the particle at 2 seconds. Firstly calculating the velocity of the particle as :

`v=(ds(t))/(dt)`

`v=(d(√(t^3+1)))/(dt)`

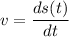
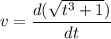
This gives,
`v=(3t^2)/(2√(t^3+1))`

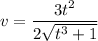
Since,
`a=(dv)/(dt)`

`a=(d((3t^2)/(2√(t^3+1))))/(dt)`

`a=(3t^4+12t)/(4(t^3+1)^(3/2))`

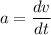
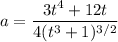
At t = 2 seconds,

`a=(3(2)^4+12(2))/(4((2)^3+1)^(3/2))`

`a=0.66\ ft/s^2`

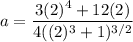
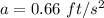
or

`a=(2)/(3)\ ft/s^2`

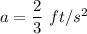
So, the acceleration of the particle at 2 seconds is 2/3 ft/s². Hence, this is the required solution.