Answer:
18.52 m
Step-by-step explanation:
When the life preserver is dropped from the helicopter, the only force acting on the object is the gravitational force. This modifies the equations of motion. Thus, the working equation is written below:
h = vt + 0.5gt²
where
v is the initial velocity
g is the acceleration due to gravity equal to 9.81 m/s²
h is the height of the fall
h = (1.46 m/s)(1.8 s) + 0.5(9.81 m/s²)
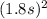
h = 18.52 m
**This is the same as the expert answer but they forgot to square the time by two**