Answer:
68.75 miles/week
Explanation:
Alan drives an average of 100 miles each week.
His car can travel an average of 25 miles per gallon of gasoline.
Gasoline consumption per week =

Cost of 1 gallon gasoline = $4
So., cost of 4 gallons gasoline = 4*4 = $16
Now, Alan would like to reduce his weekly expenditure on gasoline by $5.
The reduced cost would be:


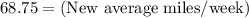
New average miles/week = 68.75 miles/week