Question

Please help me solve the triangle. A = 32°, a = 19, b = 12 by using the law of sines

Answer 1

Δ ABC: ∠A = 32° ; a = 19 (side a opposed to angle A)
and side b = 12 (opposed to Angle B)

Law of sine's
:
(sin A)/19 = (sin B)/12, but sin A = sin 32° = 0.53
0.53/19 = (sin B)/12

and sin B = (0.53 x 12) / 19 → sin B = 0.335.
Calculate ∠ B:
sin B = 0.335. → sin⁻¹(0.335) = 19.57° ≈ 20°
∠ A = 32°, ∠B ≈ 20° and ∠C = 180° -32°-20° = 128°
Now that we have got the 3 Angles, let's find c, the 3rd side of the Δ

sin 32/19 = sin 128/c
0.03 = 0.788/c and c ≈ 26
+a = 19, b = 12 an c = 26

Answer 2

a = 19, b = 12 and c = 28

Explanation:

In the ΔABC, we are given A = 32°, a = 19, b = 12.

Here we can use law of sinea and find the missing angles and sides.

The law of sines

`(a)/(sin A)` =
`(b)/(sinB)` =
`(c)/(sinC)`

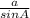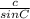
Let's find the angles first using the given information.

a/sinA = b/sinB

Now plug in a = 19, b = 12 and A = 32° and find the ∠B.

19/sin32 = 12/sinB

Cross multiplying, we get

19*sinB = 12*sin32

19*sinB = 6.359

sinB = 0.335

B = sin⁻¹(0.335) = 19.57° ≈ 20°

Now let's find the ∠C. We know that the sum of the interior angles of a triangle is 180°.

∠A + ∠B + ∠C = 180°

32° + 20° + ∠C = 180°

∠C = 180° - 52°

∠C = 128°

Now let's find the missing side c.

`(a)/(sin A)` =
`(c)/(sinC)`

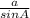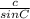
Now plug in a = 19, A = 32° and ∠C = 128° find the side c.

19/sin32 = c/sin128

Cross multiplying and simplifying, we get [Use calculator to find the value of sin32 and sin 128]

c = 28.25

c ≈ 28[Rounded to the nearest whole number]

Therefore, a = 19, b = 12 and c = 28