
is continuous over its domain, all real
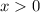
.
Meanwhile,
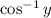
is defined for real
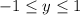
.
If
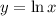
, then we have
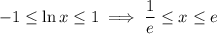
as the domain of
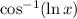
.
We know that if
and
are continuous functions, then so is the composite function

.
Both
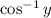
and

are continuous on their domains (excluding the endpoints in the case of
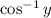
), which means
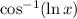
is continuous over
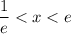
.