Answer:
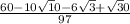
Explanation:
Hello!
To rationalize the denominator, we have to remove any root operations from the denominator.
We can do that by multiplying the numerator and denominator by the conjugate of the denominator. The conjugate simply means the same terms with different operations.
Rationalize
The answer is
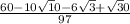 .
.