Question

PLEASE HELP I REALLY WANNA PASS , Im trying to post this image ILL GIVE A MEDAL

A group of people were surveyed, and the data about their age and hemoglobin levels was recorded in a two-way table. Based on the data in the table, match each probability with its correct value.

Answer 1

older then 35, hemo. less then 9.....76/162 = 0.47
younger then 25, hemo. above 11....69/139 = 0.50
25-35 age group, hemo. less then 9...32/128 = 0.25
older then 35, hemo. between 9 and 11...46/162 = 0.28

Answer 2

• 0.25 →→→→ The probability that a person of age group 25-35 years has a hemoglobin level less than 9.

• 0.47 →→→→ The probability that a person older than 35 years has a hemoglobin level less than 9.

• 0.28 →→→→ The probability that a person older than 35 years has a hemoglobin level between 9-11.

• 0.50 →→→→ The probability that a person younger than 25 years has a hemoglobin level above 11.

Explanation:

Tile 1:

The probability that a person older than 35 years has a hemoglobin level less than 9.

Let A denotes the event that the age of a person is above 35 years.

Let B denote the event that the hemoglobin level is less than 9.

Then A∩B denote the event that a person above 35 years has hemoglobin less than 9.

Let P denote the probability of an event.

Hence, we are asked to find:

P(B|A)

We know that:

`P(B|A)=(P(A\bigcap B))/(P(A))\\\\\\P(B|A)=((76)/(429))/((162)/(429))\\\\\\P(B|A)=(76)/(162)\\\\P(B|A)=0.47`

Tile 2:

The probability that a person younger than 25 years has a hemoglobin level above 11.

Let A denotes the event that the age of a person is less than 25 years.

Let B denote the event that the hemoglobin level is more than 11.

Then A∩B denote the event that a person below 25 years has hemoglobin more than 11.

Let P denote the probability of an event.

Hence, we are asked to find:

P(B|A)

We know that:

`P(B|A)=(P(A\bigcap B))/(P(A))\\\\\\P(B|A)=((69)/(429))/((139)/(429))\\\\\\P(B|A)=(69)/(139)\\\\P(B|A)=0.50`

Tile 3:

The probability that a person of age group 25-35 years has a hemoglobin level less than 9.

Let A denotes the event that the age of a person is of age group 25-35 years.

Let B denote the event that the hemoglobin level is less than 9.

Then A∩B denote the event that a person between 25-35 years has hemoglobin less than 9.

Let P denote the probability of an event.

Hence, we are asked to find:

P(B|A)

We know that:

`P(B|A)=(P(A\bigcap B))/(P(A))\\\\\\P(B|A)=((32)/(429))/((128)/(429))\\\\\\P(B|A)=(32)/(128)\\\\P(B|A)=0.25`

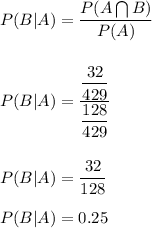
Tile 4:

The probability that a person older than 35 years has a hemoglobin level between 9-11.

Let A denotes the event that the age of a person is above 35 years.

Let B denote the event that the hemoglobin level between 9-11.

Then A∩B denote the event that a person above 35 years has hemoglobin between 9-11.

Let P denote the probability of an event.

Hence, we are asked to find:

P(B|A)

We know that:

`P(B|A)=(P(A\bigcap B))/(P(A))\\\\\\P(B|A)=((46)/(429))/((162)/(429))\\\\\\P(B|A)=(46)/(162)\\\\P(B|A)=0.28`