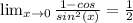Question

What is the limit of (1-cosx)/(sin^2x) and x approaches 0 (number 20 in the picture)

Answer 1

first we try to evalaute
doesn't work
so we use l'hopital's rule
because we get 0/0 or an inditerminate form when evaluting the limit

so
for f(x)/g(x), we can do f'(x)/g'(x) and evaluate again

takeing the derivitive of the top and bottom sepearely, we get

`(sin(x))/(2sin(x)cos(x))`
evaluating, we get 0/0
another inditerminate
take derivitive of top and bottom again
use chain rule
we get

`(cos(x))/(2(cos^2(x)-sin^2(x)))`
evaluating, we get 1/(2(1-0))=1/(2)=1/2



`\lim_(x \to 0)(1-cos)/(sin^2(x))=(1)/(2)`