Question

Find the standard deviation for each data set. Use the standard deviation's to compare the pair of data sets.fastest recorded speeds of various large wild cats (miles per hour)75 55 40 50 45 40 25 35 20fasted recorded speeds of various birds in flight (miles per hour)220 105 96 56 66 37 55 28 55 25 20 30The standard deviation of the large wild cats is o=0(Round the final answer to the nearest hundredth as needed. Round all intermediate values to the nearest hundredth as needed)The standard deviation of the birds in flight is o-(Round the final answer to the nearest hundredth as needed. Round all intermediate values to the nearest hundredth as needed)The stardard deviations of the two data sets show that the fastest recorded speeds of large wild cats deviate from the mean than the fastest recorded speeds of birds in flight

Answer 1

We are given the following two data sets

Fastest recorded speeds of various large wild cats (miles per hour)

75 55 40 50 45 40 25 35 20

Fastest recorded speeds of various birds in flight (miles per hour)

220 105 96 56 66 37 55 28 55 25 20 30

The standard deviation is given by

`\sigma=\sqrt[]{(1)/(N)\sum(x-\mu)^2_{}}`

Where N is the number of data points.

μ is the average/mean and x is the value of individual data points.

So first let us find the mean of each data set

Recall that mean is calculated by adding all the data points and dividing them by number of data points.

Speeds of various large wild cats:

We have 9 data points

`\mu=(75+55+40+50+45+40+25+35+20)/(9)=(385)/(9)=42.78`

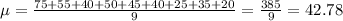
Now the standard deviation can be found as

`\sigma=15.48`

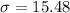
So the standard deviation of the speeds of various large wild cats is 15.48

Speeds of various birds in flight:

We have 12 data points

The mean of the data is given by

`\mu=(220+105+96+56+66+37+55+28+55+25+20+30)/(12)=(793)/(12)=66.08`

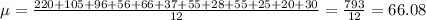
Now the standard deviation can be found just as we did before

`\sigma=53.12`

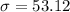
So the standard deviation of speeds of various birds in flight is 53.12.

Comparison:

As you can see, the standard deviation of speeds of various large wild cats is less as compared to the speeds of various birds in flight.