Question

Which products result in a difference of squares? Check all that apply.

(x – y)(y – x)
(6 – y)(6 – y)
(3 + xz)(–3 + xz)
(y2 – xy)(y2 + xy)
(25x – 7y)(–7y + 25x)
(64y2 + x2)(–x2 + 64y2)

Answer 1

The answers to your question is C, D, and F. These products will result in a difference of squares

Answer 2

`(3+xz)(-3+xz)`

`(y^(2)-xy)(y^(2)+xy)`

`(64y^(2)+x^(2))(-x^(2)+64y^(2))`

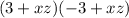
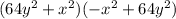
Explanation:

we know that

The difference of squares is equal to

`(a+b)(a-b)=a^(2)-b^(2)`

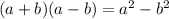
so

case A)
`(x-y)(y-x)`

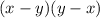
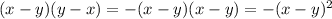`(x-y)(y-x)=-(x-y)(x-y)=-(x-y)^(2)` ------> is not a difference of squares

case B)
`(6-y)(6-y)`

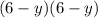
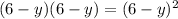`(6-y)(6-y)=(6-y)^(2)` -----> is not a difference of squares

case C)
`(3+xz)(-3+xz)`

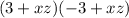
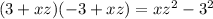`(3+xz)(-3+xz)=xz^(2)-3^(2)` -----> is a difference of squares

case D)
`(y^(2)-xy)(y^(2)+xy)`

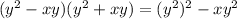`(y^(2)-xy)(y^(2)+xy)=(y^(2))^(2)-xy^(2)` -----> is a difference of squares

case E)
`(25x-7y)(-7y+25x)`

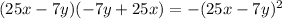`(25x-7y)(-7y+25x)=-(25x-7y)^(2)` ------> is not a difference of squares

case F)
`(64y^(2)+x^(2))(-x^(2)+64y^(2))`

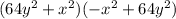
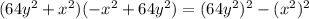`(64y^(2)+x^(2))(-x^(2)+64y^(2))=(64y^(2))^(2)-(x^(2))^(2)` -----> is a difference of squares