Question

The following values represent exponential function ƒ(x) and linear function g(x).

ƒ(1) = 2 g(1) = 2.5
ƒ(2) = 6 g(2) = 4

A. Determine whether or not there is a solution to the equation In 2-3 sentences describe whether there is a solution to the equation ƒ(x)=g(x) between x=1 and x=2.

B. Use complete sentences to justify your claim.

Answer 1

alrighty

any exponential function can be written in form
y=abˣ

we are given f(1) and f(2)
also g(1) and g(2)

to solve for the equations, we do the following:
f(2)=ab²
f(1)=ab¹
so
f(2)/f(1)=(ab²)/(ab¹)=b=6/2=3
then simple subsitution tells us that a=2/3

`f(x)=((2)/(3))(3)^x`

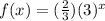
for g(x)
g(2)/f(1)=(ab²)/(ab¹)=b=4/2.5=8/5
using experimentaion, we find that

`g(x)=((25)/(16))((8)/(5))^x`



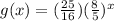
A. if we solve we get about x=1.3
that is below 1 ad 2
or, we notice that since they are polynomials, they are continous
then make a table to show that f(1)<g(1) and f(2)>g(2) so therefor they intersect somewhere beween x=1 and x=2


B. see above in the begining