Question

I need answers and steps too. please help.
additional maths

Answer 1

For this particular question, there are three specific rules that are necessary as well as the principle of reverting and obtaining logs to and from their exponential form.
Three specific rules:
1)
`log_(a) (x) - log_(a)(y) = log_(a)( (x)/(y))`
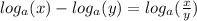
2)
`nlog_(a)(x) = log_(a)( x^(n))`
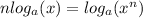
3) a⁰ = 1
Principle:

`a^(n) = b` ⇒
`n = log_(a)(b)`

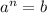
So:
Using rule 2, we can firstly write out the given logarithmic equation as:
log₇(5x) = log₇((3)⁴)
log₇(5x) = log₇(81)
Subtract log₇(81) from both sides to get:
log₇(5x) - log₇(81) = 0
Now, use rule 1 to get a single log:
log₇(5x/81) = 0
Use principle to convert this to exponential form:
7⁰ = 5x/81
Use rule 1 and solve for x:
5x/81 = 1
5x = 81
x = 81/5 = 16.2