Question

An object is thrown with an initial velocity v0 forming an angle θ with an inclined plane, which a In turn it forms an α-angle α with a horizontal plane.

A) Find the distance X from the launch point to the point where the object falls. X = F (v0, θ, α, g)

B) Find the distance for v0 = 20m / s, θ = 53o , α= 36 ° , g = 9.8m / s2

Answer 1

Refer to the figure shown below, which is based on the given figure.

d = the horizontal distance that the projectile travels.
h = the vertical distance that the projectile travels.

Part A
From the geometry, obtain
d = X cos(α) (1a)
h = X sin(α) (1b)

The vertical and horizontal components of the launch velocity are respectively
v = v₀ sin(θ - α) (2a)
u = v₀ cos(θ - α) (2b)

If the time of flight is t, then
vt - 0.5gt² = -h
or
0.5gt² - vt - h = 0 (3a)
ut = d (3b)

Substitute (1a), (1b), (2a), (2b) (3b) into (3a) to obtain

`0.5(9.8)( (d)/(u))^(2) -v_(0) sin(\theta - \alpha ) (d)/(u) - h = 0`

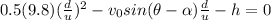
`4.9[ (X cos \alpha )/(v_(0) cos(\theta - \alpha ) ]^(2) - v_(0) sin(\theta - \alpha ) [ (X cos \alpha )/(v_(0) cos(\theta - \alpha ) ] - X sin \alpha = 0`
Hence obtain

`aX^(2)-bX=0 \\ where \\ a=4.9[ (cos \alpha )/(v_(0) cos(\theta - \alpha ))]^(2) \\ b = cos \alpha \, tan(\theta - \alpha ) + sin \alpha`
The non-triial solution for X is

`X= (b)/(a)`

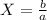
Answer:

`X= (sin \alpha + cos \alpha \, tan(\theta - \alpha ))/(4.9 [ (cos \alpha )/(v_(0) \, cos(\theta - \alpha )) ]^(2))`

Part B
v₀ = 20 m/s
θ = 53°
α = 36°

sinα + cosα tan(θ-α) = 0.8351
cosα/[v₀ cos(θ-α)] = 0.0423

X = 0.8351/(4.9*0.0423²) = 101.46 m

Answer: X = 101.5 m