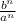neato
alrighty, there are several ways to approach this
remmeber that
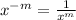
and

and
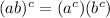
and
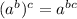
3 things we can do are
write a/b as ab⁻¹
or
distribute the -n to both a and b
or
just treat the whole thing as one fractoin
first way
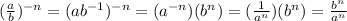
2nd way
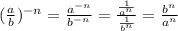
3rd way
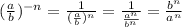
in all cases, the answer is