1 Answer

Shareema · Answer 1 · 2018-12-18T07:22:06+0000

well, first off let's take a peek of what is the slope of "y" in this case hmmm

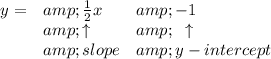
$\bf \begin{array}{llll} y=&(1)/(2)x&-1\\ &\uparrow &~\uparrow \\ &slope&y-intercept \end{array}$ so, is 1/2 ok....

now, a line that is perpendicular to that equation, will have a slope that is negative reciprocal of that.

$\bf \textit{perpendicular, negative-reciprocal slope for slope}\quad \cfrac{a}{b}\\\\ slope=\cfrac{a}{{{ b}}}\qquad negative\implies -\cfrac{a}{{{ b}}}\qquad reciprocal\implies - \cfrac{{{ b}}}{a}\\\\ -------------------------------\\\\ slope=\cfrac{1}{2}\qquad negative\implies -\cfrac{1}{{{ 2}}}\qquad reciprocal\implies - \cfrac{{{ 2}}}{1}\implies -2$

so, what is the equation of a line whose slope is -2 and passes through (0,6)?

$\bf \begin{array}{lllll} &x_1&y_1\\ % (a,b) &({{ 0}}\quad ,&{{ 6}})\quad \end{array} \\\\\\ % slope = m slope = {{ m}}= \cfrac{rise}{run} \implies -2 \\\\\\ % point-slope intercept y-{{ y_1}}={{ m}}(x-{{ x_1}})\implies y-6=-2(x-0)\\ \left. \qquad \right. \uparrow\\ \textit{point-slope form} \\\\\\ y-6=-2x\implies y=-2x+6$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

No related questions found

Other Questions