Answer:
No, it won't same.
Explanation:
Given,
The number of bulls = 18,
And, the number of cows = 45,
So, the ratio of the bulls and cow =
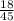 =
=
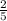
After comprising 4 more bulls and 4 more cows,
The new number of cows = 45 + 4 = 49,
While, the new number of bulls = 18 + 4 = 22,
Thus, the new ratio of bulls and cow =
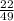
Since,

Hence, the ratio of bulls to cows will not remain the same.