Question

Dolores is arranging coffee mugs on shelves in her shop. She wants each shelf to have the same number of mugs. She only wants one color of mug on each shelf. If she has 49 blue mug and 56 red mugs what is the greatest number she can put on each shelf? How many shelves does she need for

Answer 1

Answer with explanation:

Given : Dolores each shelf to have the same number of mugs. She only wants one color of mug on each shelf.

If she has 49 blue mug and 56 red mugs then to find the greatest number she can put on each shelf, we need to find the greatest common factor of 49 and 56.

Prime factorization of 49 and 56 :-

`49=7* 7\\\\56=2*2*2*7`

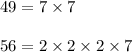
Greatest common factor of 49 and 56 = 7

∴The greatest number she can put on each shelf =7

Now, Number of shelves for blue mug =
`(49)/(7)=7`

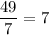
Number of shelves for red mug =
`(56)/(7)=8`

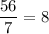
∴ Total shelves needed = 7+8=15

Answer 2

The restriction is that, there is only one color of mug per shelf. Also, each shelf must contain the same number of mugs. So, our basis will be the last number which is 49. Therefore, Dolores would need two shelves, one for the 49 blue mugs, and the other for the 49 red mugs.