The general equation of a circle is given as
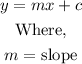
The first equation is given as
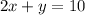
Making y the subject of the formula and then comparing coefficient
Subtract 2x from both sides
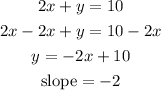
The second equation is given as
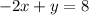
Add 2x to both sides and compare coefficients
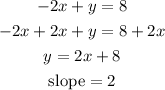
The third equation is given as
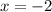
The equation above is a vertical line and hence, the slope is undefined
The fourth equation is given as
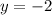
The equation above is a horizontal line and as such,the slope is zero
Considering the graph of the equation of the line attached below
Bringing out coordinates from the graph, we will have
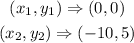
The slope of a line passing through points (x1,y1) and (x2,y2) is calculated using the formula below
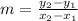
By substituting the values, we will have
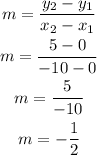
Here, the slope is = -1/2
Considering the graph of the equation of the line attached below
Bringing out coordinates from the graph, we will have
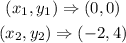
The slope of a line passing through points (x1,y1) and (x2,y2) is calculated using the formula below
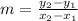
By substituting the values, we will have
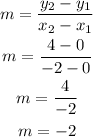
Here,the slope is = -2
Therefore,
The equation with a slope of -2 is 2x +y =10
while the graph with a slope of -2 is given below