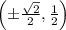Question

Find the poin on the graph 0f f(x)=1-x^2 that are closest to0(0,0)

Answer 1

Represent any point on the curve by (x, 1-x^2). The distance between (0, 0) and (x, 1-x^2) is


`√((x-0)^2+(1-x^2-0)^2)=√(x^2+(1-x^2)^2)=√(x^2+1-2x^2+x^4)`

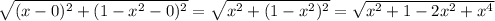
To make this easier, let's minimize the SQUARE of this quantity because when the square root is minimal, its square will be minimal.

So minimize
`L=x^4-x^2+1`

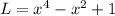
Find the derivative of L and set it equal to zero.


`(d)/(dx)(L)=4x^3-2x \\ 4x^3-2x=0 \\ 2x(2x^2-1)=0`

This gives you
`x=0` or
`x^2=(1)/(2) \\ x=\pm√(2)/2`

You can use the Second Derivative Test to figure out which value(s) produce the MINIMUM distance.


`(d^2)/(dx)=12x^2-2`

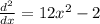
When x = 0, the second derivative is negative, indicating a relative maximum. When
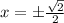
`x=\pm(√(2))/(2)`, the second derivative is positive, indicating a relative MINIMUM.

The two points on the curve closest to the origin are
`\left( \pm(√(2))/(2),(1)/(2) \right)`