Question

Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.

Five times the sum of the digits of a two-digit number is 13 less than the original number. If you reverse the digits in the two-digit number, four times the sum of its two digits is 21 less than the reversed two-digit number.

(Hint: You can use variables to represent the digits of a number. If a two-digit number has the digit x in tens place and y in one’s place, the number will be 10x + y. Reversing the order of the digits will change their place value and the reversed number will 10y + x.)

The difference of the original two-digit number and the number with reversed digits is
.

Answer 1

Let the tens digit of the original number be represented by x. Let the ones digit be y.

The original number is then 10x + y, and the reversed number is 10y + x.

"Five times the sum of the digits is 13 less than the original number" becomes:


`5(x+y)=10x+y-13`

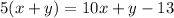
"Four times the sum of its digits is 21 less than the reversed number" becomes:


`4(x+y)=10y+x-21`

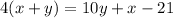
Work with the first equation until it is simpler:


`5x+5y=10x+y-13 \\ 5x-4y=13`

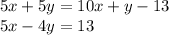
Do the same thing with the second equation:


`4x+4y=10y+x-21 \\ -3x+6y=21`

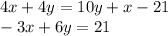
Now you have a system of two equations to solve.


`5x-4y=13 \\ -3x+6y=21`

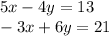
To eliminate x, multiply the first equation by 3 and multiply the second equation by 5


`15x=12y=39 \\ -15x +30y=105`

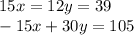
Add the two equations.


`18y=144 \\ y=8`

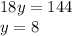
Aha! The one digit of the original number is 8. To find y, put x = 8 into any equation containing both x and y.


`5x-4(8)=13 \\ 5x-32=13 \\ 5x=45 \\ x=9`

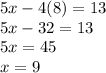
Sweet! The tens digit of the original number is 9. The original number is 98 and the reversed number is 89.

Their difference is 9.