Question

True or false? Given the linear system of equations. There is an infinite number of solutions for this linear system of equations. y=4x 4x+y=0

Answer 1

A linear system has an infinite number of solutions if the two equations describe the SAME line.

Example: y = 2x and 4x - 2y = 0. The equation 4x - 2y = 0 can be solved for y by adding 2y to both sides and then dividing by 2:


`4x-2y=0 \\ 4x=2y \\ 2x=y`

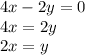
The "two" lines are really the same line, so the system has an infinite number of solutions.

Your system is y = 4x and 4x + y = 0. Is the second equation equivalent to the first?


`4x+y=0 \\ y=-4x`

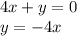
No! The statement is false.