The Solution.
Below is the given figure, which is a rhombus, since all the sides are equal.
For a rhombus, the diagonals intersect at a right angle, that is, 90 degrees.
Considering right-angled triangle DOC:
We shall find the length of the unknown diagonal by applying the Pythagorean Theorem.
![\begin{gathered} x^2+12^2=13^2 \\ x^2+144=169 \\ x^2=169-144=25 \\ \text{Taking the square root of both sides, we get} \\ x=\sqrt[]{25}=\pm5 \\ x=5\text{ (discard x=-5)} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/gqlaubntl6ozrjjwy2cz.png)
So, the unknown diagonal is
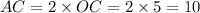
Now, the area of the given figure can be calculated with the formula below:
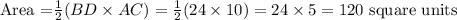
Hence, the correct answer is 120 square units.