Question

HURRY PLEASE :)!!

The triangles are similar. The area of the larger triangle is 206 ft^2. Find the area of the smaller triangle to the nearest whole number.

Answer 1

Since the triangles are similar, the ratio of the sides of larger triangle to the smaller triangle is a constant.

That constant =
`(15)/(9) = (5)/(3)`

Since the sides are in that constant proportion, the area of the triangles will also be in proportion.

(Area of larger triangle) over (Area of smaller triangle) =
`(5)/(3)`


`(206)/(x) = (5)/(3)`


`x = 206 * (3)/(5) = (618)/(5)` = 123.6 ≈ 124

Hence, to the nearest whole number the area of smaller triangle is 124 ft².

Answer 2

Area of the smaller triangle 74 ft².

Explanation:

Given : The triangles are similar. The area of the larger triangle is 206 ft^2.

To find : Find the area of the smaller triangle to the nearest whole number.

Solution : We have given that triangles are similar and area of the larger triangle is 206 ft^2.

By the similar triangles property :
`(Area\ of\ triangle 1)/(Area\ of\ triangle\ 2) = ((side\ of\ triangle\ 1)^(2))/((side\ of\ triangle\ 2)^(2) )`.

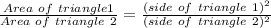Then Side of triangle 1 = 15 ft .

Side of triangle 2 = 9 ft.

Area of triangle 1 = 206 ft².

Let area of triangle 2 = x.

Then ,

Ratio of sides =
`(15)/(9)` =
`(5)/(3)`

`(206)/(x) = ((5)^(2))/((3)^(2) )`.

`(206)/(x) = ((25)/(9)`.

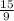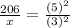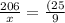On cross multiplication :

206 * 9 = 25 *x

1854 = 25 * x .

On dividing by 25

x = 74.16 ft².

Therefore, Area of the smaller triangle 74 ft².