Question

How can one third x − 2 = one fourth x + 11 be set up as a system of equations?

Answer 1

Consider the equation y=f(x), with solutions of the form (x,y)


y=f(x) means that y equals an expression in terms of x,

for example f(x) could be
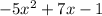
`-5x^(2)+7x-1`, or
`8√(x)- (7)/(x)`

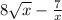
so f(x) is an expression with x'es and numbers


Given 2 equations:

i) y=f(x) and g) y=g(x)

the solutions of the system:

i. y=f(x)
ii. y=g(x)

are pairs (x,y) which satisfy both i and ii, at the same time.

to solve this system, we let f(x)=g(x).


In our problem, we are given:
`(1)/(3)(x-2)= (1)/(4)(x+11)`

since both expressions are expressions of x and some numbers,

let


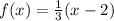
`f(x)=(1)/(3)(x-2)` and
`g(x)=(1)/(4)(x+11)`

then a system of equations is:

i)
`y=(1)/(3)(x-2)`
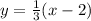
ii)
`y=(1)/(4)(x+11)`


Remark:

to find the solutions:


`(1)/(3)(x-2)= (1)/(4)(x+11)`

4(x-2)=3(x+11)

4x-8=3x+33

x=33+8=41

to find y substitute x=41 in either of the equations:

for x=41, y=1/3 (x-2) = 1/3 (41-2) =1/3 (39) = 13

[or y= 1/4 (x+11) = 1/4 (41+11)= 1/4 (52) = 13