Question

G is the centroid of triangle ABC.
What is the length of AE?

? units

Answer 1

G is the centroid it means that BG/FG=2 (G divides the median with this ratio)
3x+6/2x-1=2
3x+6=4x-2
x=8
then AG=26 then GE=13 so AE=39

Answer 2

we know that

The centroid is the intersection of the three medians in the triangle. The centroid divides each median into two parts, which are always in the ratio
`2:1`

Step 1

Find the value of x

`(BG)/(GF)=(2)/(1) \\ \\(3x+6)/(2x-1)=(2)/(1)\\ \\3x+6=2(2x-1)\\ \\3 x+6=4x-2\\ \\4 x-3x=6+2\\ \\x =8\ units`

Step 2

Find the value of GE

`(AG)/(GE)=(2)/(1) \\ \\(2x+10)/(GE)=(2)/(1)\\ \\2x+10=2GE\\\\`

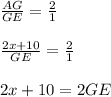
Substitute the value of x

`2x+10=2GE\\2 *8+10=2GE\\GE=13\ units`

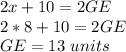
Step 3

Find the value of AE

`AE=AG+GE\\AE=(2x+10)+13\\AE=(2*8+10)+13=39\ units`

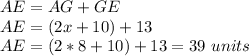
therefore

the answer is

the length of AE is
`39\ units`