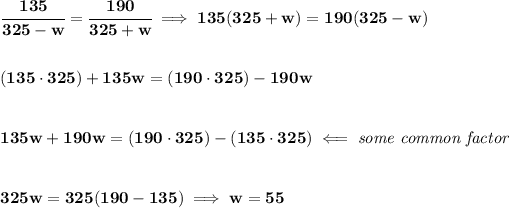Question

A plane can fly 325 mph in still air. If it can fly 190 downwind in the same amount of time it can fly 135 miles upwind, find the velocity of the wind?

Answer 1

recall your d = rt, distance = rate * time

so hmm, if say the speed rate of the wind is "w", when the plane is flying with the wind, is not really flying 325 mph, is really flying " 325 + w " fast.

now, when the plane is going against the wind, so-called upwind, is not really going 325 mph either, is really going " 325 - w " fast.

now, bear also in mind that, it took "t" hours to go one way, and it also took "t" hours to go the other way.

so.... let's check then


`\bf \begin{array}{lccclll} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ &------&------&------\\ \textit{with the wind}&190&325+w&t\\ \textit{against the wind}&135&325-w&t \end{array} \\\\\\ \begin{cases} 190=t(325+w)\implies (190)/(325+w)=\boxed{t}\\\end{cases}`


`\bf \cfrac{135}{325-w}=\cfrac{190}{325+w}\implies 135(325+w)=190(325-w) \\\\\\ (135\cdot 325)+135w=(190\cdot 325)-190w \\\\\\ 135w+190w=(190\cdot 325)-(135\cdot 325)\impliedby \textit{some common factor} \\\\\\ 325w=325(190-135)\implies w=55`