Question

NO LINKSFind the area of each regular polygon. Round your answer if necessary.

Answer 1

Since we don't know the length of the side of this hexagon, we need to find the measure of its internal angles.

Step 1. Find the measure of one internal angle of the hexagon (six side polygon). We find the measure of one internal angle A, using the following formula:

`A=(180(n-2))/(n)`

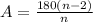
where n is the number of sides of the regular polygon. In this case:

`n=6`

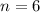
Thus, 1 internal angle "A" is equal to:

`\begin{gathered} A=(180(6-2))/(6) \\ A=(180(4))/(2) \\ A=(720)/(6) \\ A=120 \end{gathered}`

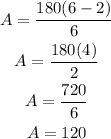
We show the measure of one internal angle in the polygon in the following image:

Step 2. Draw a right triangle using the line that is already drawn in the polygon. Note: that line is called the apothem of the polygon.

Here, note that the green angle is equal to 60 because it is half of the 120° angle.

Step 3. Use the trigonometric function tangent, to find the adjacent side to the angle of:

`\tan 60=\frac{\text{opposite side}}{adjacent\text{ side}}`

In this case, the opposite side to the 60° angle is 12, and the adjacent side is x:

thus:

`\tan 60=(12)/(x)`

Solving for x:

`\begin{gathered} x=(12)/(\tan 60) \\ x=\frac{12}{\sqrt[]{3}} \end{gathered}`

This is because tan60 is equal to the square root of 3.

Step 4. Find the length of one side of the polygon.

As we can see by the previous diagram, the side of the polygon y twice the length of x.

`\begin{gathered} l=2x \\ \end{gathered}`

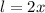
we substitute the value of x found in step 3:

`\begin{gathered} l=2(\frac{12}{\sqrt[\square]{3}}) \\ l=\frac{24}{\sqrt[]{3}} \end{gathered}`

Step 5. Now we can use the formula to calculate the area:

`A=(n\cdot l\cdot a)/(2)`

where n is the number of sides, l is the length of each side, and a is the apothem:

`\begin{gathered} n=6 \\ l=\frac{24}{\sqrt[\square]{3}} \\ a=12 \end{gathered}`

Substituting these values into the formula:

`A=\frac{6(\frac{24}{\sqrt[]{3}})(12)}{2}`

Solving the operations:

`A=498.83u^2`

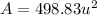
The area is 498.83 units squared.

Answer: 498.83