Question

Determine the angles made by the vector v = (67)i + (-15)j with the positive x- and y-axes. write the unit vector n in the direction of v

Answer 1

To determine the angles made by the vector v = (67)i + (-15)j with the positive x- and y-axes, use trigonometry. The unit vector n in the direction of v can be calculated by dividing each component of v by its magnitude.

Step-by-step explanation:

To determine the angles made by the vector v = (67)i + (-15)j with the positive x- and y-axes, we can use trigonometry. The angle made with the positive x-axis, which is the angle 0₁, can be found using the arctan function and the ratio of the y-component to the x-component:

0₁ = arctan((-15)/(67)) ≈ -12.67°

Similarly, the angle made with the positive y-axis, which is the angle 0j, can be found using the arctan function and the ratio of the x-component to the y-component:

0j = arctan((67)/(-15)) ≈ -76.58°

To write a unit vector n in the direction of v, divide each component of v by its magnitude:

n = (67/√((67)^2+(-15)^2))i + (-15/√((67)^2+(-15)^2))j

Answer 2

Consider the picture attached.

From right triangle trigonometry:

tan(α)=(opposite side)/(adjacent side)=15/67=0.2239

using a scientific calculator we find that arctan(0.2239)=12.62°

thus α=12.62°, is the angle that the vector makes with the positive x-axis.

The angle made with the + y-axis is 12.62°+90°=102.62°.



The length of the vector v can be determined using the Pythagorean theorem:


`|v|= \sqrt{ 67^(2) + 15^(2) }= √(4489+225)= √(4714)=68.8`


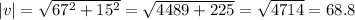
Thus, to make v a unit vector, without changing its direction, we need to divide v by |v|=68.8.

This means that the x and y components will also be divided by 68.8, by proportionality.

So, the unit vector in the direction of v is:

(67/68.8)i + (-15/68.8)j=0.97 i + (- 0.22)j


Answer: 12.62°; 102.62°; 0.97 i + (- 0.22)j