Question

PLEASE HELP!
Calculate $40^{13} \pmod{85}.$

Answer 1

In this type of calculations, we decompose 13 by checking the lowest powers of the base, that is 40. for example we check 40^2, or 40^3 and compare it to 85

Notice

40*40*40=64,000

so we check how many time does 85 fit into 64,000:

64,000/85=752.94

85*753=64,005; 64000-64,005=-5

this means that


`40^(3) =-5\pmod{85}`

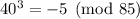
thus


`40^(13) =40^(3*4+1)={(40^(3))}^(4)*40=(-5)^(4)*40 \pmod{85}=\\\\625*40\pmod{85}=(7*85+30)*40\pmod{85}=30*40\pmod{85}\\\\=1200\pmod{85}=(14*85+10)\pmod{85}=10\pmod{85}`


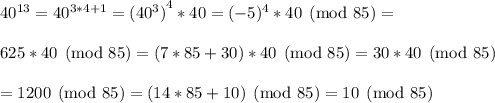
Answer: 10 (mod85)

Remark, the set of all solutions is:

{......-75, 10, 95, .....}, that is 85k +10