Question

How do i find the quadratic equation using the points(-2,5)(-1,2)(0,1)

Answer 1

We have points (-2,5), (-1,2) and (0,1) and we need to find the quadratic equation that pass through these 3 points.

We have 3 parameters to find, but, if we look at the points the point (0,1) is already telling us the y-intercept (the value of y when x=0).

Then, c=1.

We can then start with the function as:

`y=ax^2+bx+c=ax^2+bx+1`

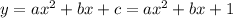
Replacing the values of (x,y) for the remaining 2 points we will get a system of equations with two equations and two unknowns:

For point (-2,5)

`\begin{gathered} (x,y)=(-2,5) \\ 5=a\cdot(-2)^2+b\cdot(-2)+1 \\ 5=4a-2b+1 \\ 5-1=4a-2b \\ 4a-2b=4 \end{gathered}`

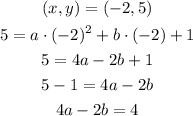
For point (-1,2)

`\begin{gathered} (x,y)=(-1,2) \\ 2=a(-1)^2+b(-1)+1 \\ 2=a-b+1 \\ 2-1=a-b \\ a-b=1 \end{gathered}`

Then, we have the equations:

`\begin{gathered} 4a-2b=4 \\ a-b=1 \end{gathered}`

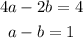
We can solve it by elimination as:

`\begin{gathered} (4a-2b)-2(a-b)=4-2(1) \\ 4a-2b-2a+2b=2 \\ 4a-2a-2b+2b=2 \\ 2a+0b=2 \\ 2a=2 \\ a=1 \end{gathered}`
`\begin{gathered} a-b=1 \\ 1-b=1 \\ b=1-1 \\ b=0 \end{gathered}`

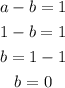
With a=1 and b=0, the equation becomes:

`y=1x^2+0x+1=x^2+1`

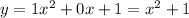
Answer: y=x^2+1

NOTE: 3 points to determine the quadratic equation.

We have points (x1,y1), (x2,y2) and (x3,y3).

Then we can write for each one:

`\begin{gathered} y_1=a\cdot x^{2_{}}_1+b\cdot x_1+c \\ y_2=a\cdot x^{2_{}}_2+b\cdot x_2+c \\ y_1=a\cdot x^{2_{}}_2+b\cdot x_2+c \end{gathered}`

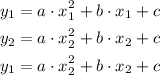
That would give us a 3 equations - 3 unknown system, being a, b and c the unknowns we have to solve:

`\begin{gathered} (x_1)^2\cdot a+(x_1)\cdot b+(1)\cdot c=y_1 \\ (x_2)^2\cdot a+(x_2)\cdot b+(1)\cdot c=y_2 \\ (x_3)^2\cdot a+(x_3)\cdot b+(1)\cdot c=y_3 \end{gathered}`

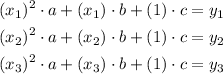
For example, with points (-2,5), (-1,2) and (0,1) we would get:

`\begin{gathered} (-2)^2\cdot a+(-2)\cdot b+1\cdot c=5\longrightarrow4a-2b+c=5 \\ (-1)^2\cdot a+(-1)\cdot b+1\cdot c=2\longrightarrow a-b+c=2 \\ (0)^2\cdot a+(0)+1\cdot c=1\longrightarrow c=1 \end{gathered}`

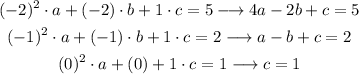
The last equation gives us the c coefficient directly (c=1), and then we can solve it from there as we did.