ANSWER :
a. y = 3 feet
b. The maximum height is 19 feet
c. 33.44 ft
EXPLANATION :
From the problem, we have the equation :
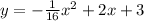
a. The height of the ball, y when x = 0 is :
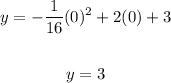
b. The maximum height can be obtained by substitute x = h
where h is :
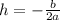
Solve for h with a = -1/16 and b = 2
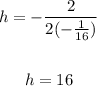
Substitute x = h = 16, then solve for y :
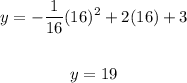
c. The distance of the ball to the child when the ball strikes the ground is when y = 0
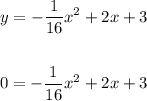
Using quadratic formula with a = -1/16, b = 2 and c = 3
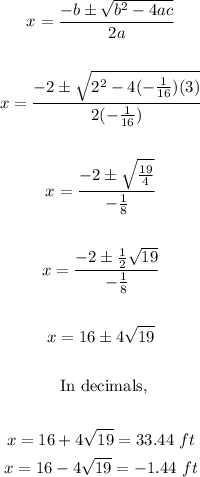
Since there's no negative distance, the answer will be 33.44 ft