Question

5 people enter a racquetball tournament in which each person must play evert other person exactly once. Determine the total number of games that will be played

Answer 1

This is the "handshake problem", namely with n people, how many handshakes will there be if every will shake hands with everyone else.
n people will shake hands with (n-1) other people. Since we are counting twice for each handshake, the number of handshakes is n(n-1)/2.
For n=5, the number of matches is 5(5-1)/2=10.
This is also the number of diagonals in an n-sided convex polygon.

Answer 2

The total number of games that will be played is 10.

Explanation:

Consider the provided information.

There are 5 people and each person must play evert other person exactly once.

Each time 2 team will play together out of 5.

It is all possible pairings of the 5 players or 5 objects taken 2 at a time.

So we can solve it as:

`(5!)/(2!(5-2)!) =(5!)/(2!3!) \\(4* 5)/(2)=10`

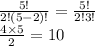
Hence, the total number of games that will be played is 10.