Question

Calculate the perimeter and area of the shape. Round to two decimal places.

Answer 1

Part 1: Solve for Perimeter of the shape.

To solve for the perimeter, add the length of the three sides of the bottom section of the figure which resembles a rectangle, and add it to half the circumference of the arc on the top section.

`\begin{gathered} \text{To solve for the perimeter of the half circle, divide the formula for circumference by 2} \\ C=(2\pi r)/(2)=\pi r \\ \text{the radius is half of 35 in.} \\ C=\pi(17.5\text{ in}) \\ C=54.98\text{ in.} \end{gathered}`

Add the result to the three sides of the bottom section

`\begin{gathered} P=54.98\text{ in}+50\text{ in}+35\text{ in}+50\text{ in} \\ P=189.98\text{ in} \\ \\ \text{Therefore, the perimeter of the given shape is 189.98 inches.} \end{gathered}`

Part 2: Solve for the area of the shape.

The shape can be divided into two sections of shape, a rectangle in the bottom, and half a circle on top. We can find the area by adding the area of the rectangle, and the semicircle.

`A_{\text{total}}=A_{\text{rectangle}}+A_{\text{semicircle}}`

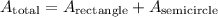
Given dimensions for the rectangle is

length = 50 inches

width = 35 inches

radius = 17.5 inches (half of the width)

`\begin{gathered} A_{\text{total}}=A_{\text{rectangle}}+A_{\text{semicircle}} \\ A_{\text{total}}=lw+(\pi r^2)/(2) \\ A_{\text{total}}=(50\text{ in})(35\text{ in})+\frac{\pi(17.5\text{ in}^2}{2} \\ A_{\text{total}}=1750\text{ in}^2+\frac{\pi(306.25\text{ in}^2)}{2} \\ A_{\text{total}}=1750\text{ in}^2+\pi(153.125\text{ in}^2) \\ A_{\text{total}}=1750\text{ in}^2+481.06\text{ in}^2 \\ A_{\text{total}}=2231.06\text{ in}^2 \\ \\ \text{Therefore, the area of the shape is }2231.06\text{ in}^2 \end{gathered}`