Part 1: Solve for Perimeter of the shape.
To solve for the perimeter, add the length of the three sides of the bottom section of the figure which resembles a rectangle, and add it to half the circumference of the arc on the top section.
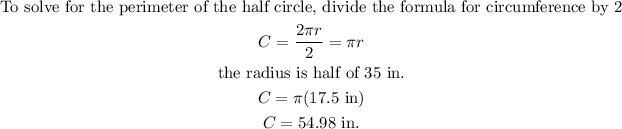
Add the result to the three sides of the bottom section
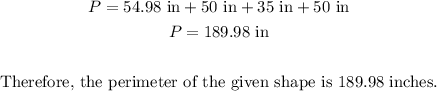
Part 2: Solve for the area of the shape.
The shape can be divided into two sections of shape, a rectangle in the bottom, and half a circle on top. We can find the area by adding the area of the rectangle, and the semicircle.
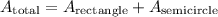
Given dimensions for the rectangle is
length = 50 inches
width = 35 inches
radius = 17.5 inches (half of the width)
