Question

A fuel pump sends gasoline from a car's fuel tank to the engine at a rate of 5.64 10-2 kg/s. the density of the gasoline is 735 kg/m3, and the radius of the fuel line is 3.43 10-3 m. what is the speed at which the gasoline moves through the fuel line?

Answer 1

The speed is
`2.076(m)/(s)`

Step-by-step explanation:

We have the data of the gasoline pumping rate.

The gasoline pumping rate indicates the amount of gasoline per unit of time that the fuel pump sends to the car's fuel tank. We indicate the gasoline pumping rate with
`GPR`

`GPR=(5.64).10^(-2)(kg)/(s)`

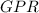
Its units are
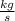`(kg)/(s)` which are units of mass over time
`((m)/(t))`

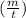
The density of the gasoline is
`735(kg)/(m^(3))`

The density is equal to
`(mass)/(volume)=(m)/(v)`

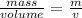
If we divide the GPR by the density we obtain :

`(GPR)/(density)=(m/t)/(m/v)=(v)/(t)=(volume)/(time)`

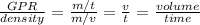
Where
`(v)/(t)` is the volume flow rate (VFR) :

`VFR=((5.64).10^(-2)(kg)/(s))/(735(kg)/(m^(3)))=(7.6735).10^(-5)(m^(3))/(s)`

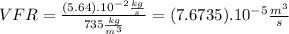
The VFR is equal to area per speed.

`VFR=(area).(speed)=A.S`

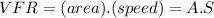
The area (A) is equal to
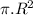`\pi.R^(2)` given that the fuel line is circular.

`A=\pi.R^(2)=\pi.[(3.43).10^(-3)m]^(2)=(3.6960).10^(-5)m^(2)`

Now we have the VFR and A. The final step is to calculate the speed (S) :

`VFR=A.S`

`S=(VFR)/(A)`

`S=((7.6735).10^(-5)(m^(3))/(s))/((3.6960).10^(-5)m^(2))=2.076(m)/(s)`

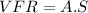
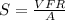
The speed of the gasoline is
`2.076(m)/(s)`

Answer 2

Given:
Gasoline pumping rate, R = 5.64 x 10⁻² kg/s
Density of gasoline, D = 735 kg/m³
Radius of fuel line, r = 3.43 x 10⁻³ m

Calculate the cross sectional area of the fuel line.
A = πr² = π(3.43 x 10⁻³ m)² = 3.6961 x 10⁻⁵ m²

Let v = speed of pumping the gasoline, m/s
Then the mass flow rate is
M = AvD = (3.6961 x 10⁻⁵ m²)*(v m/s)*(735 kg/m³) = 0.027166v kg/s

The gasoline pumping rate is given as 5.64 x 10⁻² kg/s, therefore
0.027166v = 0.0564
v = 2.076 m/s

Answer: 2.076 m/s
The gasoline moves through the fuel line at 2.076 m/s.