Question

Find an equation of a sphere if one of its diameters has endpoints (2, 3, 5) and (6, 5, 7).

Answer 1

Note that the distance, d, between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) in a 3-dimensional rectangular system is

`d = \sqrt{(x_(2)-x_(1))^(2) + (y_(2)-y{1})^(2)+(z_(2)-z_(1))^(2)}`

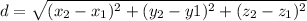
Therefore, the length of the diameter of the sphere is

`d = \sqrt{(6-2)^(2)+(5-3)^(2)+(7-5)^(2)} = √(24)`
The radius is
r = d/2 = √(24)/2=√6
or
r² = 6

The center of the sphere is

`( (2+6)/(2), (3+5)/(2), (5+7)/(2)) = (4, 4, 6).`

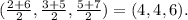
Answer:
The equation of the sphere is
(x-4)² + (y-4)² + (z-6)² = 6