Question

Suppose ∠A and ∠B are complementary angles, m∠A = (3x + 5)°, and m∠B = (2x – 15)°. Solve for x and then find m∠A and m∠B

Answer 1

Two angles are complementary when they add up to 90° ⇒

∠A + ∠B = 90°
3x + 5 + 2x - 15 = 90
5x - 10 = 90
5x = 90 + 10
5x = 100
x = 100/5
x = 20

m∠A = 3x + 5 = 3*20 + 5 = 60 + 5 = 65°
m∠B = 2x - 15 = 2*20 - 15 = 40 - 15 = 25°

Answer 2

`x=20`

`m\angle A=65`

`m\angle B=25`

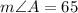
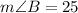
Explanation:

We have been given that ∠A and ∠B are complementary angles. The measure of angle A is
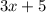`3x+5` degrees and measure of angle B is
`2x-15` degrees.

We know that complementary angles add up-to 90 degrees, so we can set an equation as:

`3x+5+2x-15=90`

`5x-10=90`

`5x-10+10=90+10`

`5x=100`

`(5x)/(5)=(100)/(5)`

`x=20`

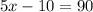
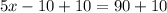
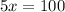
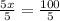
Therefore, the value of x is 20.

`m\angle A=3x+5`

`m\angle A=3(20)+5`

`m\angle A=60+5`

`m\angle A=65`

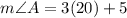
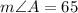
Therefore, the measure of angle A is 65 degrees.

`m\angle B=2x-15`

`m\angle B=2(20)-15`

`m\angle B=40-15`

`m\angle B=25`

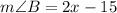
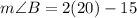
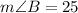
Therefore, the measure of angle B is 25 degrees.