Question

Create a logarithmic expression that has four log terms added or substracted together and highlights the three log properties in this section that are used to simplify logs. After creating the expression, use the log properties to simplify your expression to a single log. Make sure to explain which property is being used.

Answer 1

We have

`\log (5x)+\log (7x)-\log (2x)-\log (4x)`

We will use the next properties

`\log (a)+\log (b)=\log (ab)`
`\log (a)-\log (b)=\log ((a)/(b))`

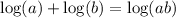
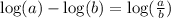
Then we apply the properties

Here we use the first property two simplify the first two terms

`\begin{gathered} \log (5x\cdot7x)-\log (2x)-\log (4x) \\ \log (35x^2)-\log (2x)-\log (4x) \\ \end{gathered}`

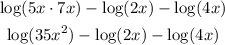
Here we use the second property to simplify the first three terms

`\begin{gathered} \log ((35x^2)/(2x))-\log (4x) \\ \log ((35x)/(2))-\log (4x) \end{gathered}`

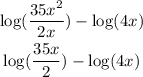
Here we use the second property to simplify the whole expression

`\log (((35x)/(2))/(4x))=\log ((35)/(8))`

ANSWER

log(35/8)