Question

Choose the equation below that represents the line passing through the point (−5, 1) with a slope of three halves.

A y − 5 = three halves(x + 1)
B y + 1 = three halves(x − 5)
C y + 5 = three halves(x − 1)
D y − 1 = three halves(x + 5)

Answer 1

Answer 2

Answer: The correct option is D, i.e., y − 1 = three halves(x + 5).

Step-by-step explanation:

It is given that the line passing through the point (−5, 1) with a slope of three halves.

The equation of line passing through the point
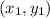`(x_1,y_1)` with slope m is defined as,

`y-y_1=m(x-x_1)`

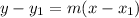
It is a point slope form.

Since we have point (-5,1) and slope three halves. Put these value in the above point slope form.

`y-1=\text{three halves}(x-(-5))`

`y-1=\text{three halves}(x+5)`

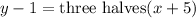
This equation is same as equation is shown in option D, therefore the option D is correct.