Question

Determine whether the vectors u and v are parallel, orthogonal, or neither. u = <7, -4>, v = <-28, 16>

Answer 1

hmmm to tell if they're orthogonal(perpendicular) to each other, we can simply get their dot-product, if their dot-product is 0, then they indeed are perpendicular, let's check


`\bf \ \textless \ 7,-4\ \textgreater \ \cdot \ \textless \ -28,16\ \textgreater \ \implies (7\cdot -28)+(-4\cdot 16)\implies -190`

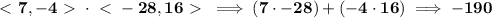
well, no luck there... now, let's introspect the digits a little


`\bf \begin{array}{llll} \ \textless \ 7,-4\ \textgreater \ \qquad \ \textless \ &-28,&16\ \textgreater \ \\ &~~\uparrow &~\uparrow \\ &-4\cdot 7&-4\cdot -4 \end{array}`

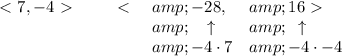
notice, the second vector, -28, 16, is just a multiple of the first one, that simply means, they're parallel.

you can always just do a b/a check and simplify both vectors, if they yield the same ratio, they're parallel, since they're just multiples of each other.