Question

The leg of a right triangle is 2 units and the hypotenuse is 4 units. What is the length, in units, of the other leg of the triangle?

Answer 1

The equation for a right triangle is a^2+b^2=c^2. The hypotenuse is c. The leg can be a or b. The equation you now have is 2^2+b^2=4^2. Do the exponents. You get 4+b^2=16. Subtract 4 from each side to get b^2=12. Sqaure root each side to get b=3.4641 units. So the length of the other leg of the triangle is 3.4641 units. Hope this helps! ;)

Answer 2

Other side = 2
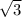`√(3)` or
`√(12)`

Explanation:

Given : The leg of a right triangle is 2 units and the hypotenuse is 4 units.

To find : What is the length, in units, of the other leg of the triangle.

Solution : We have given

Leg of a right triangle = 2 units.

Hypotenuse = 4 units.

By the Pythagorean theorem :

(Hypotenuse)² = (One leg)² + (other leg)².

Plug the values,

(4)² = (2)² + (other leg)².

16 = 4 + (other leg)².

On subtracting both sides by 4

16 - 4 = (other leg)².

12 = (other leg)².

Taking square root.

Other sides =
`√(12)`.

Other sides =
`√(4 *3)`.

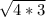Other side = 2
`√(3)`.

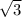Therefore, Other side = 2
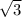`√(3)` or
`√(12)`