Question

Find three positive integers x, y, and z that satisfy the given conditions. the product is 64, and the sum is a minimum.

Answer 1

Minimize
`x+y+z` subject to
`xyz=64`. Using Lagrange multipliers, we can take the Lagrangian


`L(x,y,z,\lambda)=x+y+z+\lambda(xyz-64)`

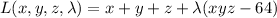
which has partial derivatives (set to 0)


`\begin{cases}L_x=1+\lambda yz=0\\L_y=1+\lambda xz=0\\L_z=1+\lambda xy=0\\L_\lambda=xyz-64=0\implies xyz=64\end{cases}`

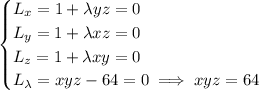
From the first three equations, pick any two and subtract them from one another. You'll arrive at the following symmetric relations:


`\begin{cases}(1+\lambda yz)-(1+\lambda xz)=0\implies \lambda(y-x)z=0\\\lambda(z-y)x=0\\\lambda(z-x)y=0\end{cases}`

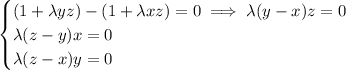
We assume
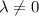
`\lambda\\eq0`, and we know that
`xyz=64` so that we can omit the possibilities of
`x=0`,
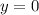
`y=0`, and
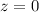
`z=0`. This leaves us with
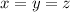
`x=y=z`, and so


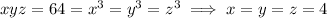
`xyz=64=x^3=y^3=z^3\implies x=y=z=4`.