Question

Freddie is at chess practice waiting on his opponent's next move. He notices that the 4-inch-long minute hand is rotating around the clock and marking off time like degrees on a unit circle.

Part 1: How many radians does the minute hand move from 3:35 to 3:55? (Hint: Find the number of degrees per minute first.)
Part 2: How far does the tip of the minute hand travel during that time?
You must show all of your work.

Answer 1

One complete revolution of the minute hand sweeps a central angle of 360° which is equivalent to 60 minutes.
That is, the minute hand creates
(360°/(60 min) = 6 degrees/min.

From 3:35 to 3:55 is 20 minutes.
It sweeps a central angle of
(20 min)*(6 deg/min) = 120°

Because 360° = 2π radians,
120° = (120/360)*2π = (2π)/3 radians

Answer:

`(2 \pi )/(3) \,radians`
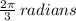
In decimals, this is 2.1 radians (nearest tenth)

Part 2:
Because the minute hand is 4 inches long, the length of the arc swept is
(4 in)*(2π/3 radians) = 8π/3 inches

Answer:

`(8 \pi )/(3) \,inches`
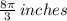
In decimals, this is 8.4 inches (nearest tenth).