The value of x is
![\[ x = (r \cdot w)/(u) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8bx418sglpi9x1mwhqyu.png) .Therefore, option A is correct
.Therefore, option A is correct
To determine if the two triangles in the image are similar, we need to compare their corresponding angles. For triangles to be similar, all corresponding angles must be congruent (equal in measure) and the sides must be in proportion.
From the image, we can see:
Triangle
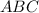 :
:
- Angle
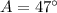
- Angle
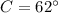
Triangle DEF:
- Angle
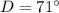
- Angle
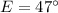
We can calculate the third angle of each triangle using the fact that the sum of angles in a triangle is
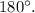
For triangle
Angle
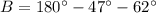
For triangle DEF:
Angle

Let's calculate these angles. If all the corresponding angles match, the triangles are similar.
The third angles of the triangles are as follows:
- For triangle
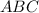 , angle
, angle
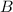 is
is
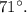
- For triangle DEF, angle
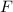 is
is
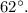
Comparing corresponding angles of the two triangles:
- Angles
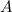 and
and
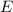 are both
are both
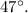
- Angles
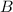 and
and
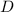 are both
are both
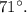
- Angles
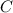 and
and
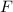 are both
are both
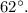
Since all corresponding angles are congruent, triangles
 and DEF are indeed similar.
and DEF are indeed similar.
Now, to find the appropriate expression to solve for
 (the side corresponding to side
(the side corresponding to side
 in triangle
in triangle
 and to side
and to side
 in triangle DEF, we can use the property that corresponding sides of similar triangles are in proportion. The correct proportion will be the ratio of the sides opposite equal angles.
in triangle DEF, we can use the property that corresponding sides of similar triangles are in proportion. The correct proportion will be the ratio of the sides opposite equal angles.
Hence, the correct expression, using the sides opposite the
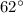 angles in both triangles, is:
angles in both triangles, is:
![\[ x = (r \cdot w)/(u) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8bx418sglpi9x1mwhqyu.png)
Therefore, the correct choice is:
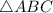

 DEF; x =
DEF; x =
![(r \cdot w)/(u) ]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/d63ti8w821ixdzdu7mqq.png)
The complete question is given below:
Decide whether the triangles are similar. If so, determine the appropriate expression to solve for x.
Triangles ABC and EDF, where triangle ABC has angle A measuring 47 degrees, angle C measuring 62 degrees, side AC labeled as y, side AB labeled as w, and side BC labeled as x and triangle EDF has angle D measuring 71 degrees, angle E measuring 47 degrees, side DE labeled z, side EF labeled u, and side DF labeled r
The triangles are not similar; no expression for x can be found.
ΔABC ~ ΔDEF; x equals r times w over u
ΔABC ~ ΔEDF; x equals r times w over u
ΔABC ~ ΔEDF; x equals r times w over z