Answer:
The height of the building does the ladder reach is 13.75 ft.
Explanation:
Given : A painter leans a 15 ft ladder against a building. The base of the ladder is 6 ft from the building.
To find : How high on the building does the ladder reach?
Solution :
Let us take AC=Length of a ladder =15 ft
BC = Distance between ladder base and wall of a building = 6 ft
AB = Height of the building does the ladder reach =h
Triangle formed is angle ABC which is right angle triangle.
Applying the Pythagoras theorem,
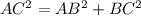
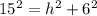

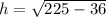
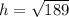
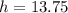
Therefore, The height of the building does the ladder reach is 13.75 ft.